神经网络学习_反向传播与梯度下降(2)
神经网络学习_反向传播与梯度下降(2)
前言
本节数学推导较多,然而是必经之路。
前向计算
我们从一个简单的神经元模型开始:
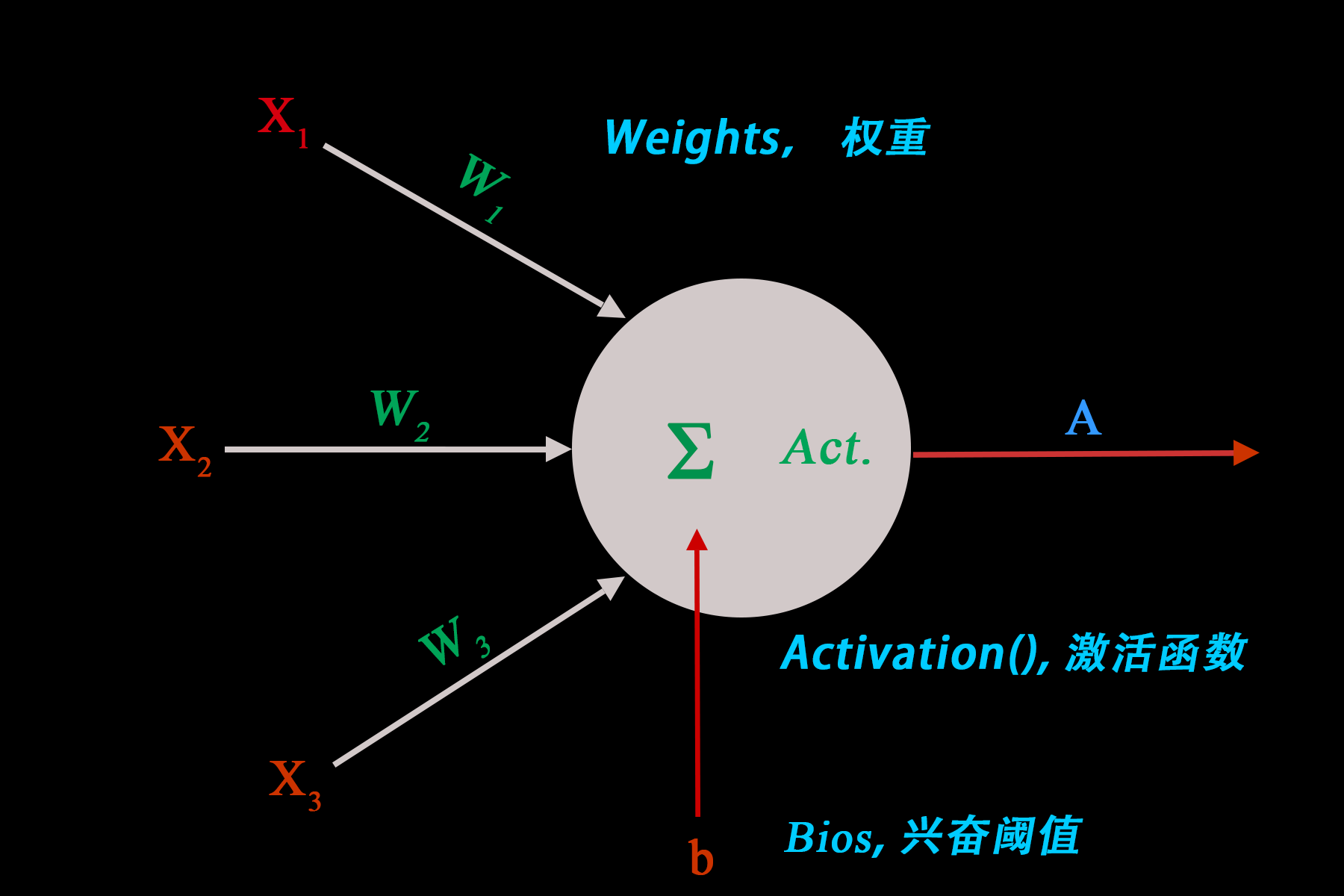
从输入到输出的计算过程是这样的: \[ \begin{align} &Z=\sum_{i=1}^{3}W_iX_i+b\\ &A=Activation(Z) \end{align} \] 神经元数量一多,整体的计算就显得特别复杂,因此我们采用矩阵乘法来简化计算: \[ \begin{bmatrix} W_1 & W_2 & W_3 \end{bmatrix} \begin{bmatrix} X_1 \\ X_2 \\ X_3 \end{bmatrix} +b =\sum_{i=1}^{3}W_iX_i+b \]
左行右列,对应相乘。
对于单层两个神经元:
第一个: \[
\begin{bmatrix}
W_{11} & W_{21} & W_{31}
\end{bmatrix}
\begin{bmatrix}
X_1 \\ X_2 \\ X_3
\end{bmatrix}
+b_1
=\sum_{i=1}^{3}W_{i1}X_i+b_1
\] 第二个: \[
\begin{bmatrix}
W_{12} & W_{22} & W_{32}
\end{bmatrix}
\begin{bmatrix}
X_1 \\ X_2 \\ X_3
\end{bmatrix}
+b_2
=\sum_{i=1}^{3}W_{i2}X_i+b_2
\] 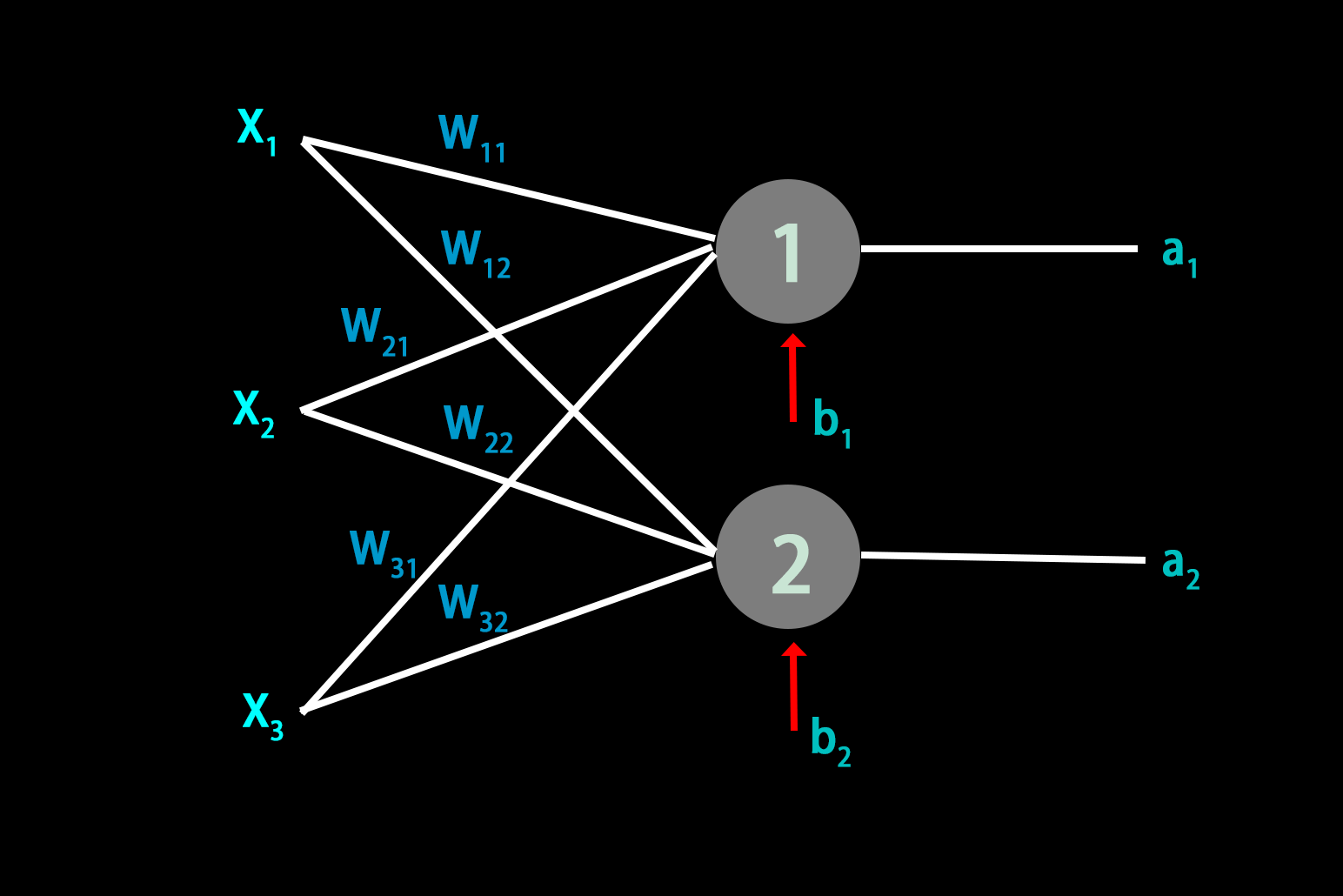
把两个结合到一起: \[ \begin{bmatrix} W_{11} & W_{21} & W_{31} \\ W_{12} & W_{22} & W_{32} \end{bmatrix} \begin{bmatrix} X_1 \\ X_2 \\ X_3 \end{bmatrix} + \begin{bmatrix} b_1 \\ b_2 \end{bmatrix} = \begin{bmatrix} \sum_{i=1}^{3}W_{i1}X_i+b_1 \\ \sum_{i=1}^{3}W_{i2}X_i+b_2 \end{bmatrix} \]
用 \(X\) 表示 \(\begin{bmatrix}X_1 \\ X_2 \\ X_3\end{bmatrix}\),\(B\) 表示 \(\begin{bmatrix}b_1 \\b_2\end{bmatrix}\),\(Z\) 表示 \(\begin{bmatrix}\sum_{i=1}^{3}W_{i1}X_i+b_1 \\\sum_{i=1}^{3}W_{i2}X_i+b_2\end{bmatrix}\)
我们一般用 \(W_{ij}\) 表示矩阵 \(W\) 第 \(i\) 行第 \(j\) 列的元素。
但是(6)式中,\(W_{ij}\) 表示的意思是:前一层的第 \(i\) 个神经元与后一层的第 \(j\) 个神经元之间的权重。
为保持下标一致,我们用 \(W\) 表示 \(\begin{bmatrix}W_{11} & W_{12} \\ W_{21} & W_{22} \\ W_{31} & W_{32}\end{bmatrix}\),\(W\) 的转置 \(W^\top\) 表示 \(\begin{bmatrix}W_{11} & W_{21} & W_{31} \\W_{12} & W_{22} & W_{32}\end{bmatrix}\) \[ \Rightarrow Z=W^\top X+B \]
注意观察这些矩阵的行数与列数。
进而可以推广到含有 \(n^{(l)}\) 个神经元的第 \(l\) 层的前向计算:
| 符号 | 说明 |
|---|---|
| \(l\) | \(\mathbb{N}^* \cup \{0\}\)。层号,第 \(0\) 层表示输入层。 |
| \(n^{(l)}\) | \(\mathbb{N}^*\)。第 \(l\) 层的神经元数量。 |
| \(Y^{(l-1)}\) | \(\mathbb{R}^{n^{(l-1)}\times1}\)。第 \(l-1\) 层的输出矩阵,同时也是第 \(l\) 层的输入矩阵。 |
| \(W^{(l)}\) | \(\mathbb{R}^{n^{(l-1)}\times n^{(l)}}\)。第 \(l-1\) 层与第 \(l\) 层之间的权重矩阵 |
| \(B^{(l)}\) | \(\mathbb{R}^{n^{(l)}\times1}\)。第 \(l\) 层的偏置(Bios)矩阵 |
| \(Act()\) | 激活函数 |
\[ \begin{align} &Z^{(l)}=(W^{(l)})^\top Y^{(l-1)}+B^{(l)}\\ &Y^{(l)}=Act(Z^{(l)}) \end{align} \]
反向传播
我们来看一个简单的三层神经网络。其中,输入层只负责将输入数据传递给隐藏层。
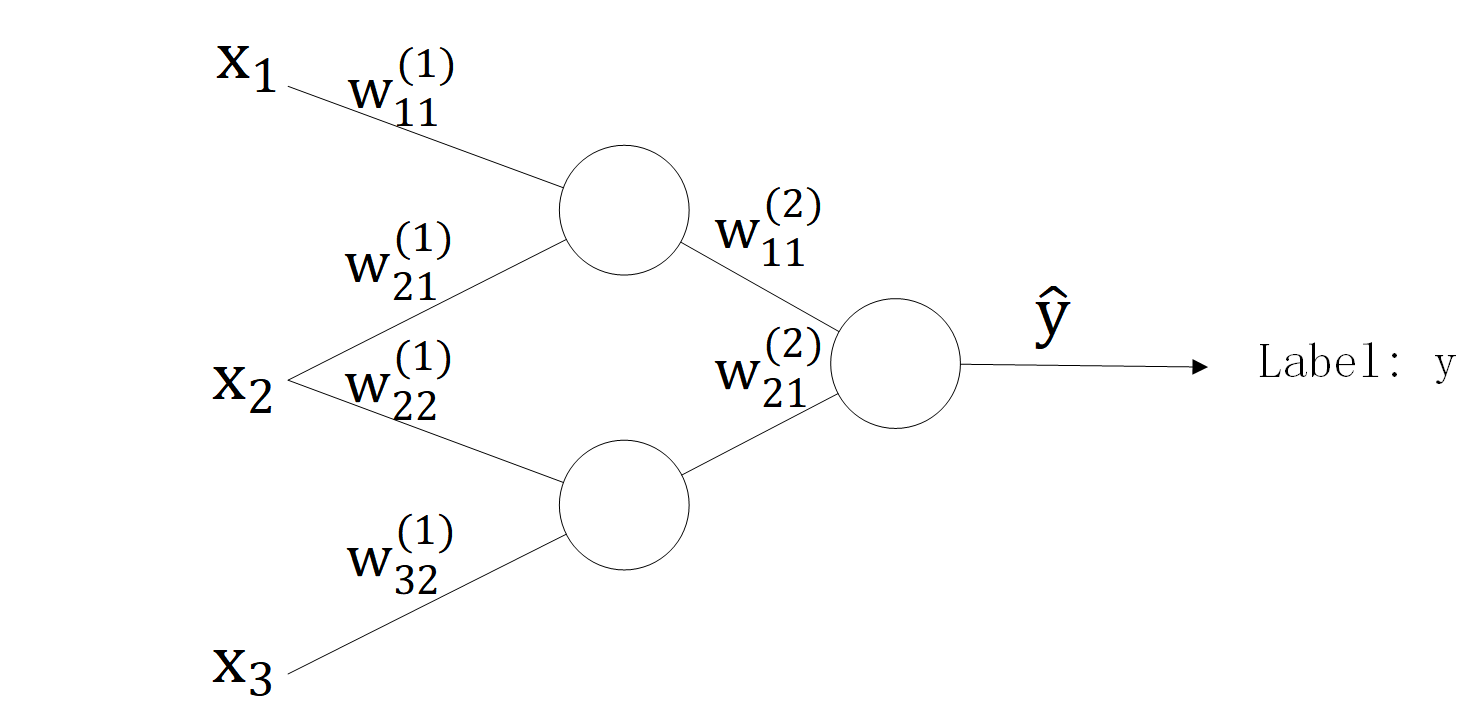
| 符号 | 说明 |
|---|---|
| \(X\) | \(\mathbb{R}^{3\times1}\)。输入层的输入。 |
| \(W^{(1)}\) | \(\mathbb{R}^{3\times2}\)。输入层与隐藏层之间的权重矩阵。 |
| \(B^{(1)}\) | \(\mathbb{R}^{2\times1}\)。隐藏层的偏置矩阵。 |
| \(Y^{(1)}\) | \(\mathbb{R}^{2\times1}\)。隐藏层的输出。 |
| \(W^{(2)}\) | \(\mathbb{R}^{2\times1}\)。隐藏层与输出层之间的权重矩阵。 |
| \(B^{(2)}\) | \(\mathbb{R}^{1\times1}\)。输出层的偏置矩阵。 |
| \(\widehat Y\) | \(\mathbb{R}^{1\times1}\)。输出层的输出。 |
| \(Y\) | \(\mathbb{R}^{1\times1}\)。准确值或标签值。 |
| \(Loss(y,\hat y)\) | 损失函数。实际输出与标签值之间的“差距”。 |
| \(Act(Z)\) | 激活函数。 |
| \(\lambda\) | 学习率。 |
当我们前向计算出实际输出 \(\widehat Y\) 后,需要与标签值 \(Y\) 比较,看二者差距是多少。因此一次前向计算后能够得到一个“差距”:\(Loss(Y,\widehat Y)\)。
我们的目标很明确,就是使得这个 \(Loss(Y,\widehat Y)\) 尽可能地小。根据前面的梯度下降法,问题就转变成了:求 \(Loss(Y,\widehat Y)\)的极小值点。
考虑到神经网络中可调整的变量就是各个权重 \(W^{(l)}\) 和偏置 \(B^{(l)}\),我们先以 \(W^{(2)}_{11}\) 为例:
简单的例子
目标
改变 \(w^{(2)}_{11}\) 使得 \(Loss(Y,\widehat Y)\) 取得极小值。
方法
\[ w^{(2)'}_{11}=w^{(2)}_{11}-\lambda \nabla Loss(Y,\widehat Y) \]
计算
梯度的计算: \[ \nabla Loss(Y,\widehat Y)=\frac{\partial{Loss(Y,\widehat Y)}}{\partial{w^{(2)}_{11}}} \] 求导的链式法则:
\({Loss(Y,\widehat Y)}\) 是 \(\widehat Y\) 的函数;
\(\widehat Y=Act(Z^{(2)})\);
\(Z^{(2)}=(W^{(2)})^\top Y^{(1)}+B^{(2)}=\sum_{i=1}^2w^{(2)}_{i1}y^{(1)}_{i1}+b^{(2)}_{11}\)
\[ \begin{align} \frac{\partial{Loss(Y,\widehat Y)}}{\partial{w^{(2)}_{11}}} =&\frac{\partial{Loss(Y,\widehat Y)}}{\partial{\widehat Y}}\cdot\frac{\partial{\widehat Y}}{\partial{Z^{(2)}}}\cdot\frac{\partial{Z^{(2)}}} {\partial{w^{(2)}_{11}}}\\ =&\frac{\partial{Loss(Y,\widehat Y)}}{\partial{\widehat Y}}\cdot\frac{\partial{Act(Z^{(2)})}}{\partial{Z^{(2)}}}\cdot \begin{bmatrix}y^{(1)}_{11}\end{bmatrix} \end{align} \] 因此: \[ w^{(2)'}_{11}=w^{(2)}_{11}-\lambda\cdot\frac{\partial{Loss(Y,\widehat Y)}}{\partial{\widehat Y}}\cdot\frac{\partial{Act(Z^{(2)})}}{\partial{Z^{(2)}}}\cdot \begin{bmatrix}y^{(1)}_{11}\end{bmatrix} \]
规定:
| 符号 | 说明 |
|---|---|
| \(Loss(y,\widehat y)=\frac{1}{2}(y-\widehat y)^2\) | 平方损失函数 |
| \(Act(x)=\frac{1}{1+e^{-x}}\) | Sigmoid 函数 |
则: \[ \frac{\partial{Loss(y,\widehat y)}}{\partial{\widehat y}}=-(y-\widehat y) \]
\[ \frac{\partial{Act(x)}}{\partial{x}}=Act(x)\cdot(1-Act(x)) \]
\[ \therefore w^{(2)'}_{11}=w^{(2)}_{11}+\lambda\cdot(Y-\widehat Y)\cdot Act(Z^{(2)})\cdot[1-Act(Z^{(2)})]\cdot\begin{bmatrix}y^{(1)}_{11}\end{bmatrix} \]
转化为矩阵形式: \[ W^{(2)'}=W^{(2)}+\lambda\cdot(Y-\widehat Y)\cdot Act(Z^{(2)})[1-Act(Z^{(2)})]\cdot Y^{(1)} \]
\(Y\in\mathbb{R}^{1\times1}\)
\(\widehat Y\in\mathbb{R}^{1\times1}\)
\(Z^{(2)}\in\mathbb{R}^{1\times1}\)
\(Act(Z^{(2)})=\begin{bmatrix}Act(z^{(2)}_{11})\end{bmatrix}\in\mathbb{R}^{1\times1}\)
\(Y^{(1)}\in\mathbb{R}^{2\times1}\)
通用的公式更为复杂,但这里并不涉及与之相关的矩阵求导。
又一个简单的例子
上一个例子中,我们得到了根据输出层的损失 \(Loss(Y,\widehat Y)\) 修改 \(W^{(2)}\) 的方法。
在这个例子中,我们将看到,输出层的损失 \(Loss(Y,\widehat Y)\) 是如何被输入层与隐藏层之间的权重 \(W^{(1)}\) 影响的。
需要注意的是: \[ Loss(Y,\widehat Y)\\ \widehat Y=Act(Z^{(2)})=Act((W^{(2)})^\top Y^{(1)}+B^{(2)})\\ Y^{(1)}=Act(Z^{(1)})=Act((W^{(1)})^\top X+B^{(1)}) \] 也就是说,\(Loss\) 并不是直接由 \(W^{(1)}\) 的计算结果得来的,它们中间还隔了一层。
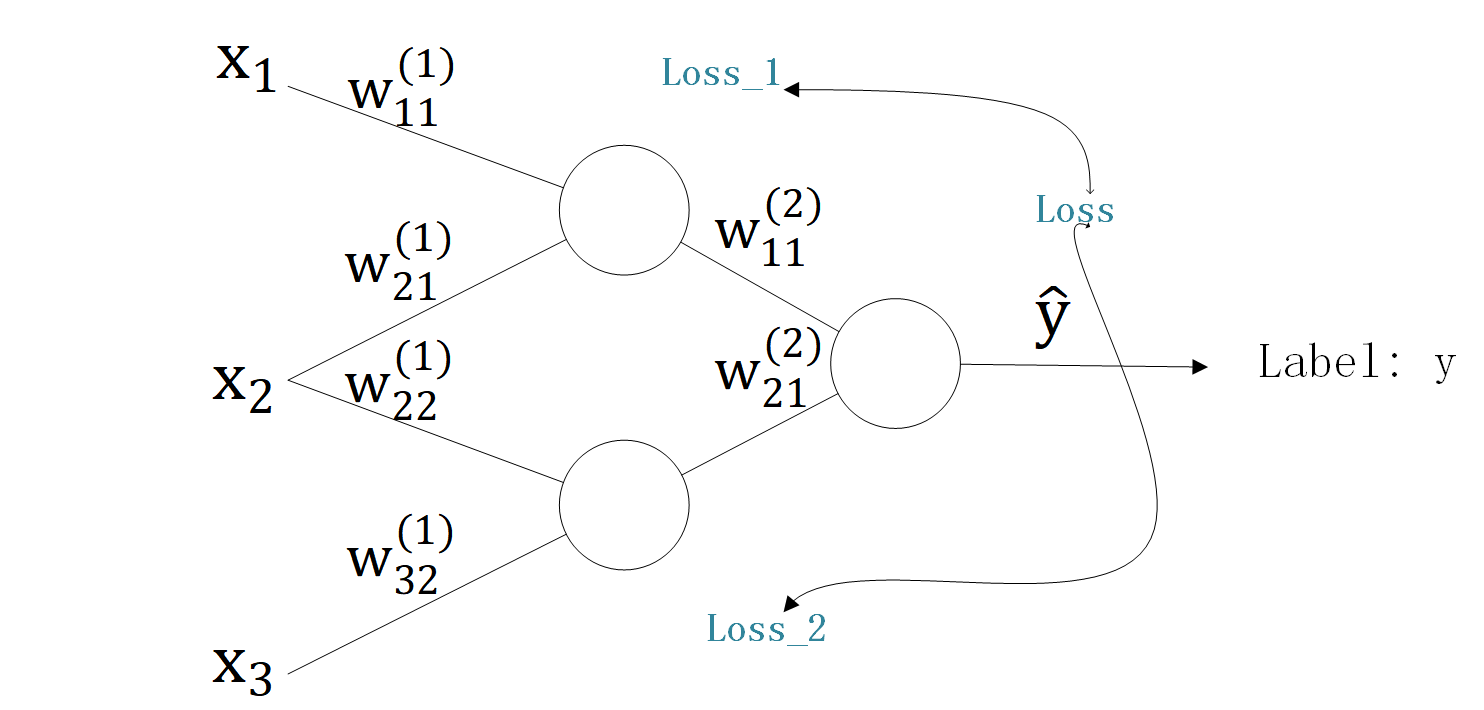
计算如下: \[ \nabla Loss(Y,\widehat Y)=\frac{\partial{Loss(Y,\widehat Y)}}{\partial{W^{(1)}}}=\frac{\partial{Loss(Y,\widehat Y)}}{\partial{}Z^{(1)}}\cdot\frac{\partial{Z^{(1)}}}{\partial{W^{(1)}}} \]
\[ \because\frac{\partial{Loss(Y,\widehat Y)}}{\partial{Z^{(1)}}}=\frac{\partial{Loss(Y,\widehat Y)}}{\partial{Z^{(2)}}}\cdot\frac{\partial{Z^{(2)}}}{\partial{Y^{(1)}}}\cdot\frac{\partial{Y^{(1)}}}{\partial{Z^{(1)}}} \]
\[ \therefore \begin{align} \nabla Loss(Y,\widehat Y)&=\frac{\partial{Loss(Y,\widehat Y)}}{\partial{W^{(1)}}}\\ &=\frac{\partial{Loss(Y,\widehat Y)}}{\partial{Z^{(2)}}}\cdot\frac{\partial{Z^{(2)}}}{\partial{Y^{(1)}}}\cdot\frac{\partial{Y^{(1)}}}{\partial{Z^{(1)}}}\cdot\frac{\partial{Z^{(1)}}}{\partial{W^{(1)}}}\\ &=\frac{\partial{Loss(Y,\widehat Y)}}{\partial{Z^{(2)}}}\cdot (W^{(2)})^\top\cdot\frac{\partial{Y^{(1)}}}{\partial{Z^{(1)}}}\cdot\frac{\partial{Z^{(1)}}}{\partial{W^{(1)}}} \end{align} \]
注意到:
\(\frac{\partial{Loss(Y,\widehat Y)}}{\partial{Z^{(2)}}}\) 可以看成最终损失对于第 \(2\) 层(输出层)激活前的值的敏感度,而 \(\frac{\partial{Loss(Y,\widehat Y)}}{\partial{Z^{(2)}}}\cdot W^{(2)}\) 将敏感度按照权重分配到了第 \(2\) 层(隐藏层)的激活后输出 \(Y^{(1)}\) 上。
其中,第 \(2\) 层共有 \(n\) 个神经元,第 \(3\) 层(输出层)共有 \(q\) 个神经元。\(W^{(2)}\in\mathbb{R}^{n\times q},\;Loss\in\mathbb{R}^{q\times1},\;Z^{(2)}\in\mathbb{R}^{q\times1}\)。则(26)式按照权重将最终损失的敏感度分配到第 \(2\) 层。
针对我们选取的激活函数和损失函数,具体形式推导如下: \[ \begin{align} W^{(1)'} &=W^{(1)}-\lambda\nabla Loss(Y,\widehat Y)\\ &=W^{(1)}+\lambda\cdot\frac{\partial{Loss(Y,\widehat Y)}}{\partial{Z^{(2)}}}\cdot (W^{(2)})^\top\cdot\frac{\partial{Y^{(1)}}}{\partial{Z^{(1)}}}\cdot\frac{\partial{Z^{(1)}}}{\partial{W^{(1)}}} \end{align} \] 带入具体函数的偏导数,得到: \[ W^{(1)'}=W^{(1)}+\lambda\cdot(Y-\widehat Y)\cdot(W^{(2)})^\top\cdot Act(Z^{(1)})[1-Act(Z^{(1)})]\cdot X \] 这就是我们的三层神经网络中,输入层与隐藏层之间的权重矩阵的调整的公式。
上面的推导并没有很好地显示出反向传播的含义。更为专业地推导可以参见CMU等的公开课。
小小的总结
回顾一下我们对于激活函数和损失函数的设定:
| 符号 | 说明 |
|---|---|
| \(Loss(y,\widehat y)=\frac{1}{2}(y-\widehat y)^2\) | 平方损失函数 |
| \(Act(x)=\frac{1}{1+e^{-x}}\) | Sigmoid 函数 |
通过上面两个例子,我们得到了三层神经网络中,在梯度下降算法下,两个权重矩阵如何进行调整: \[ W^{(2)'}=W^{(2)}+\lambda\cdot(Y-\widehat Y)\cdot Act(Z^{(2)})[1-Act(Z^{(2)})]\cdot Y^{(1)} \]
\[ W^{(1)'}=W^{(1)}+\lambda\cdot\Big[(Y-\widehat Y)\cdot(W^{(2)})^\top\Big]\cdot Act(Z^{(1)})[1-Act(Z^{(1)})]\cdot X \]
接下来便是代码实现了。
代码实现
上一节中,我们定义了神经网络类,但是还没有写它的方法。下面就添加进训练及查询的方法。需要注意的是,数学公式很简洁(虽然笔者的很丑陋。。。),实现起来很复杂。因为你不但需要考虑 Python 中的数据类型,还要考虑各种可能对神经网络的效果有很大影响的细节。
1 | # 定义神经网络类 |
后记
不得不说,自己推导真累。。。
前后纠结了两天,补了补矩阵运算😱(我已经忘得差不多了),看了看还没学的矩阵求导(一知半解)