Survival Analysis

Posted on Edited on In Views:
Symbols count in article: 4.4k Reading time ≈ 4 mins.
生存分析学习笔记

Survival Analysis

生存分析研究对象的“生存时间”的分布情况，并探究实验条件对于生存时间的影响。

生存分析的目标，就是通过对已经发生的事件的观察，来分析和预测事件在观察对象上的发生情况。通过生存分析，我们希望能够得到研究对象的生存情况在时间上的特点，估计生存率和平均生存时间，进而研究影响生存时间和观察时间发生的保护因素和不利因素。

最初应用于医学研究中，研究病人确诊后能过生存多长时间，治愈后多长时间会复发等。“生存”还可以指机器零件的损坏情况、服务的客户流失度、预测信息在社交网络的传播程度等。

概念

  • Survival Time 生存时间：从某一起点到所关心事件发生的时间。例如，研究零件的损坏情况，则关心零件何时损坏，生存时间就是从零件刚刚投入使用，到零件损坏的时间。

    但是，由于观察对象和观察时间的限制，有时候无法确定起点，有时候结束观察时对象也没有到达终点。

  • Initial Event 起始事件：反映生存时间起始特征的事件。例如疾病确证。

  • Failure Event 失效事件：反映生存时间结束特征的事件。例如病人死亡。

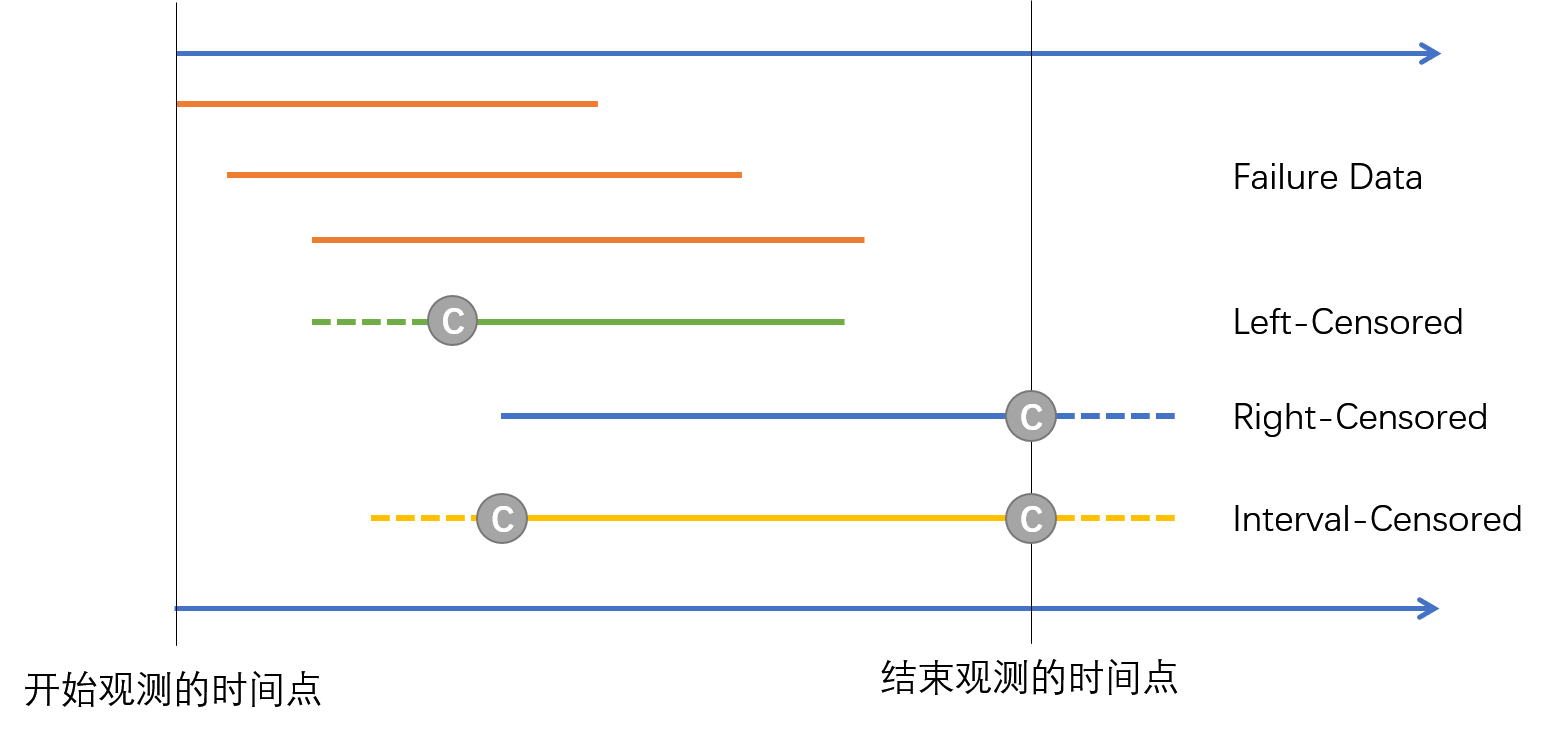
  • Censored 删失/失访：事件的发生没有或无法被观测到，导致 Survival Time 不准确的情况。可分为：

    • Left-Censored 左删失：起始时间没有被观测到，只能确定在某一个时间点之前。则记录的 Survival Time 偏小。
    • Right-Censored 右删失：结束时间没有被观测到，只能确定在某一个时间点之后。则记录的 Survival Time 偏小。
    • Interval-Censored 区间删失：始末时间都没有被观测到。

  • Failure Data 非删失数据：准确观测到始末时间的样本数据。

F: Failure Data

L: Left-Censored

R: Right-Censored

I: Interval-Censored

Censored

  • Survival Function 生存函数：观察对象生存时间 \(T\) 长于时间 \(t\) 的概率，累积生存率 \(S(t)\)。\(S(t)=P\;(T>t)\)。

  • Hazard Function 风险函数：观察对象在时刻 t 死亡的概率，瞬时死亡率 \(h(t)\)。

    \(h(t)\) 即观察对象在时刻 \(t\) 之前还没有发生任何失效事件的情况下，在时刻 \(t\) 发生失效事件的可能性。

    \[ \text{累积风险函数：}F(t)=1-S(t) \]

    \[ \text{风险概率密度函数：}f(t)=\frac{\mathrm{d}F(t)}{\mathrm{d}t}=\lim_{\Delta t\to0}\frac{F(t+\Delta t)-F(t)}{\Delta t} \]

    \[ h(t)=\lim_{\Delta t\to0}\frac{P(t\leq T\leq t+\Delta t|T\geq t)}{\Delta t}=\frac{f(t)}{S(t)}=\lim_{\Delta t\to0}\frac{S(t)-S(t+\Delta t)}{S(t)\cdot\Delta t} \]

模型

一般分为非参数模型、半参数模型和参数模型。

  • 非参数模型：不对生存时间的分布作出假设，检验危险因素对生存时间的影响采用的是非参数检验方法。无法建立生存时间与危险因素之间的关系模型。常用的有 Kaplan-Meier survival estimate KM生存曲线估计、寿命表法。

  • 参数模型：根据样本观测值估计假设分布模型中的参数，获得生存时间的概率分布模型。能够更好地分析生存数据中其他参数对于生存时间的影响。

    参数回归模型（Parametric Regression Modeling，简称 PRM）

  • 半参数模型：主要有 Cox’ s Proportional Hazards Regression Model 比例风险回归模型、Accelerated Failure Time (AFT) 加速失效模型、Shared Frailty Model 共享脆弱模型。

Kaplan-Merier 方法

\[ S(t_i)=S(t_{i-1})\cdot(1-\frac{d_i}{n_i}) \]

  1. \(S(t_i)\)：在 \(t_i\) 时刻的存活概率。
  2. \(n_i\)：在 \(t_i\) 时刻前还存活的样本数。
  3. \(d_i\)：在 \(t_i\) 时刻发生失效事件的样本数。
  4. \(t_0=0,\;S(0)=1\)

Example

共 6 个样本。

Survival Time Delta \(S(t)\) Description
10 1 \(=1\cdot(1-\frac{1}{6})=\frac{5}{6}\) 时刻 10 有 1 个样本发生失效事件，其余 5 个样本存活。
14 1 \(=\frac{5}{6}\cdot(1-\frac{1}{5})=\frac{2}{3}\) 时刻 14 有 1 个样本发生失效事件，其余 4 个样本存活。
25 0 \(=\frac{2}{3}\cdot(1-\frac{0}{4})=\frac{2}{3}\) 删失数据。该样本在时刻 25 必然生存，对于该时刻的生存率无影响。
28 1 \(=\frac{2}{3}\cdot(1-\frac{1}{4})=\frac{1}{2}\) 时刻 28 有 1 个样本发生失效事件，其余 3 个样本存活。
31 0 \(=\frac{1}{2}\cdot(1-\frac{0}{3})=\frac{1}{2}\) 删失数据。该样本在时刻 31 必然生存，对于该时刻的生存率无影响。
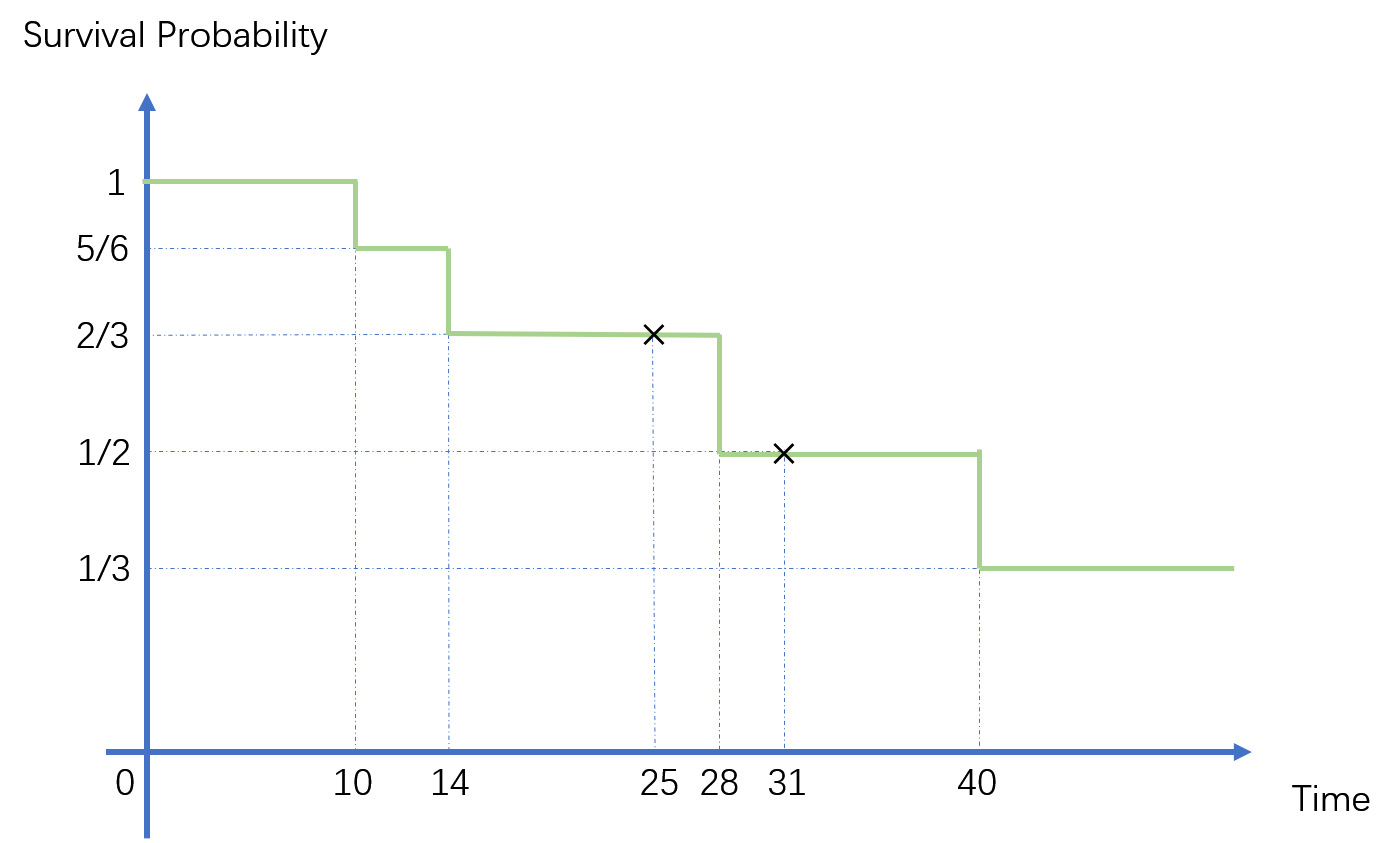
40 1 \(=\frac{1}{2}\cdot(1-\frac{1}{3})=\frac{1}{3}\) 时刻 40 有 1 个样本发生失效事件，其余 2 个样本存活。

delta = 0: right-censored;

delta = 1: complete data.

绘出生存曲线如下：

survival curve

Log-Rand Test

不同组的生存曲线是否具有显著性差异。 \[ \chi^2=\sum\frac{(A-T)^2}{T} \]

  1. \(A\)：观测死亡数。
  2. \(T\)：理论死亡数。
  3. 自由度 \(df=组数-1\)

Cox Proportional Hazards Regression

描述不随时间变化的多个特征对于某一时刻的风险函数的影响。

例如，研究人的寿命长短，即时刻 t 死亡的概率时，假设会受到人类固有寿命、健康状况、基因等的影响。

概念

  • 输入变量：也称协变量，不随时间变化。\(X=(x_1,x_2,...,x_m)\)

  • 参数：输入变量的参数。\(\beta=(\beta_1,\beta_2,...,\beta_m)^T\)

  • 生存函数：输入为 \(X\) 时，在 t 时刻仍然存活的概率。\(S(t,X)=P(T>t,X)\)

  • 死亡函数：输入为 \(X\) 时，在 t 时刻已经死亡的概率。\(F(t,X)=1-P(T\leq t,X)\)

  • 死亡密度函数：输入为 \(X\) 时，在 t 时刻死亡的概率。 \[ f(t,X)=\lim_{\Delta t\to0}\frac{P(t<T<t+\Delta t,X)}{\Delta t} \]

  • 风险函数：输入为 \(X\) 时，已经生存到了 t 时刻，但是在 t 时刻死亡的概率。 \[ \begin{align} h(t,X)&=\lim_{\Delta t\to0}\frac{P(t<T<t+\Delta t|T>t,X)}{\Delta t}\\&=\frac{f(t,X)}{S(t,X)} \end{align} \]

模型内容

\[ h(t,X_i)=\lambda_0(t)\cdot \exp(X_i\beta) \]

\(\lambda_0(t)\) 为时间相关的基准风险率，可以灵活选择。通常选择 Weibull 分布。

\[ \ln{(h(t,X))}=\beta\cdot X+\ln{(\lambda_0(t))} \]

由公式（10）得出模型的基本假设：

  1. 输入变量 \(X\) 对于风险的影响与时间无关，即 Proportional hazards 比例风险假设；
  2. 对数风险与输入变量 \(X\) 呈线性相关。

参数的MLE

由于存在 \(\lambda_0(t)\)，为半参数模型，因此使用 部分似然函数 partial likelihood： \[ L_p(\beta)=\prod_{i=1}^mL_i \] 假设 4 个失效事件分别在时刻 1, 3, 7(×), 12 发生，则：

  1. \(t=1\)，对象 1 发生失效事件，其余对象存活，且对象 1 发生失效事件的可能性最大，即 \(\max{\frac{h(1,X_1)}{h(1,X_2)+h(1,X_3)+h(1,X_4)}}\)；
  2. 同理，\(t=3\)，\(\max{\frac{h(3,X_2)}{h(3,X_3)+h(3,X_4)}}\)；
  3. \(t=7\) 为删失数据，不记录；
  4. \(t=12\) 时，无存活对象，分母不存在了，因此每一项的分母添加一个分子项。

\[ \begin{align} L_p(beta)=&\prod_{i=1}^3L_i\\ =&\frac{h(1,X_1)}{h(1,X_1)+h(1,X_2)+h(1,X_3)+h(1,X_4)}\times\\ &\frac{h(3,X_2)}{h(3,X_2)+h(3,X_3)+h(3,X_4)}\times\frac{h(12,X_4)}{h(12,X_4)}\\ =&\frac{\exp{(\beta\cdot X_1)}}{\exp{(\beta\cdot X_1)}+\exp{(\beta\cdot X_2)}+\exp{(\beta\cdot X_3)}+\exp{(\beta\cdot X_4)}}\cdot\\ &\frac{\exp{(\beta\cdot X_2)}}{\exp{(\beta\cdot X_2)}+\exp{(\beta\cdot X_3)}+\exp{(\beta\cdot X_4)}}\cdot\frac{\exp{(\beta\cdot X_4)}}{\exp{(\beta\cdot X_4)}} \end{align} \]

因此，对于 m 个失效事件，n 个完全数据，部分似然函数为： \[ L_p(\beta)=\prod_{i=1}^n\frac{\exp(\beta\cdot X_i)}{\sum_{j:t_j\geq t_i}\exp(\beta\cdot X_j)} \] 对数部分似然函数为： \[ \ln{(L_p(\beta))}=\sum_{i=1}^n\bigg[\beta\cdot X_i-\ln{\big(\sum_{j:t_j\geq t_i}\exp(\beta\cdot X_j)\big)}\bigg] \] 可利用梯度下降法等方法学习 \(\beta\)。

Accelerate Failure Time Model (AFT)

参数模型，做回归。