新型冠状病毒SIR模型分析
2019-nCov的传染病模型
Kermack-McKendrick SIR模型
该模型假定同质混合,即每个人都以均等的机会从感染者那里感染疾病,其必要条件为群体总数N趋近于无穷大。
但是同质混合忽略了居民聚集区以及社交网络的影响,可以归纳成三个变量:
- 高度聚集的个体数
- 个体间的接近程度
- 接触频率
这三个变量其实已经在暗示着,可以将该模型应用到网络(Network)上(计算机病毒、网络传染病等)。
网络传染病:考虑了现实人口的非均匀结构的传染病分析对象。
本节只分析最简单的同质混合的SIR模型。
简述
SIR(susceptible-infected-removed)模型:群体中的每个个体一般会经历的几个状态:
易感(susceptible)、感染(infected)、康复(removed)和消亡(dead)。
graph LR A["S(易感)"] --"gamma"--> B["I(感染)"] B --delta--> C["R(康复)"] B --"1-delta"--> D["死亡"]
分析
基本假设
- 人群总数为
N,\(\lim\limits_{N \to +\infty}\); - 定义易感个体数为
S(t),感染个体数为I(t),康复个体数为R(t),时间为t,感染率为\(\gamma\),恢复率(或死亡率)为\(\Delta\); - 在有限的人群中:
N = S(t) + I(t) + R(t); - 每单位时间(天/d)内,每一个易感个体和感染个体都能完成随机均匀的接触(同质混合,尽管有点不现实,但是我们从简单开始);
- 不考虑康复者的再次感染(根据初步研究,2019-nCov康复者的体内抗体在个体正常情况下能保持2-3月);
建立方程
\[ \frac{\partial{S(t)}}{\partial{t}}=-\gamma S(t)I(t) \]
\[ \frac{\partial{I(t)}}{\partial{t}}=\gamma S(t)I(t)-\Delta I(t) \]
\[ \frac{\partial{R(t)}}{\partial{t}}=\Delta I(t) \]
\[ N=S(t)+I(t)+R(t) \]
定义初始条件为: \[ S(0)=S_0\\I(0)=I_0\\R(0)=R_0 \]
方程解释
对于微分方程(1),我们想象水池中有\(S_0\)个白球和\(I_0\)个红球,根据假设4,每单位时间内,所有白球和红球能够产生\(S_0I_0\)次碰撞,每次碰撞有\(\gamma\)的机率使得白球变成红球,因此可以得到以下式子: \[ S_{d+1}=S_d-\gamma S_dI_d \]
对于连续的微分方程(1),我们选取合适的
step使其离散化,这里的step就是1天。
方程(1)表示,随着疫情的发展,易感人群数量随着\(S(t)\)和\(I(t)\)的上升而下降。
微分方程(2)、(3)很好理解。
方程(4)表示人群总数与这三个状态的人群数量无关,总保持为一个常数。
方程求解与结果分析
使用标准化的\(S\)、\(I\)、\(R\): \[ s=\frac{S(t)}{N}\\i=\frac{I(t)}{N}\\r=\frac{R(t)}{N} \] 这样使得解在区间\([0,1]\)内而不是在更复杂的\([0,n]\)内。
得到以下微分方程: \[ \frac{\partial{s}}{\partial{t}}=-\gamma si \]
\[ \frac{\partial{i}}{\partial{t}}=\gamma si-\Delta i \]
\[ \frac{\partial{r}}{\partial{t}}=\Delta i \]
\[ s+i+r=1 \]
有初始条件: \[ s(0)=s_0\\i(0)=i_0\\r(0)=r_0 \]
特例解释
我们假设\(\Delta=0\),\(s+i=1\),即排除康复或死亡的可能,每一位感染者在分析时间内都将持续存在。那么可以求解我们最关心的\(i\)关于时间\(t\)的函数: \[ \frac{\partial{i}}{\partial{t}}=\gamma (1-i)i \] 分离变量: \[ \frac{\partial{i}}{(1-i)i}=\gamma \partial{t} \] 积分: \[ \begin{align} \int_{i_0}^{i}\frac{\partial{i}}{(1-i)i}=&\int_{i_0}^{i}(\frac{1}{i}+\frac{1}{1-i})\partial{i}\\=&\int_{0}^{t}\gamma \partial{t} \end{align} \] 最后得到如下式子: \[ \ln{i}-\ln{i_0}-\ln{(1-i)}+\ln{(1-i_0)}=\gamma t \] 令\(A=\frac{1-i_0}{i_0}\),则可以求解\(i(t)\): \[ i(t)=\frac{1}{1+A\exp(-\gamma t)}\;\;\;,t\geq 0 \] 这就是逻辑斯蒂增长曲线,说明在\(\Delta=0\),\(s+i=1\)条件下,微分方程组的解\(i(t)\)落在上面。
也即SI模型。
R语言求解
模拟算法求解
我们使用一个较为冷门的packages: GillespieSSA2。它使用Gillespie的随机模拟算法('SSA')来模拟大型系统。具体介绍在这里。
注意,运行本篇中的代码前,请先确认R的环境变量(路径)中没有空格,否则可能会引发错误。另外,程序运行期间,RStudio会提示安装RBuildTools(100+MB)。
定义求解所需参数:
img_name: 图像标题params: SIR模型参数final_time: 求解的时间范围(最大时间,单位为d)initial_state: 模型初始值,置为500位易感者,1位感染者和0位康复者
根据德国哥廷根大学于晓华教授提供的参数,亦即\(\beta = 0.2586\)和\(\gamma = 0.0821\)求解模型
1 | library(GillespieSSA2) |
定义易感者转化为感染者和感染者康复的反应,也即模型方程组:
1 | reactions <- list( |
使用精确方法进行模拟:
也可以使用Explict tau-leap或Binomial tau-leap方法模拟,只需修改method参数为ssa_etl()或ssa_btl()。
1 | set.seed(1) |
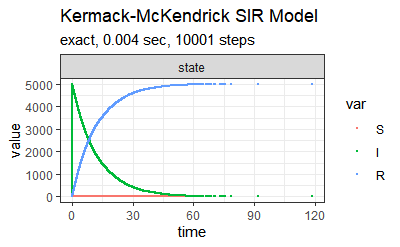
上述方法在\(\beta \approx 0.001, S=500\)时表现出与实际情况较为吻合的结果,推测是因为当\(S\)很大时,SIR模型同质混合的特点会放大感染个体的感染能力,表现在\(\beta\)较设定值高出许多。因此降低\(\beta, S\)的值能够得到较为合理的结果。
deSolver求解
接下来使用deSolver package直接求解该初值问题。deSolver具体介绍在这里。
定义SIR函数: 1
2
3
4
5
6
7
8
9
10
11library(deSolve)
library(ggplot2)
sir <- function(time, state, params){
with(as.list(c(state, params)), {
dS <- -beta * S * I
dI <- beta * S * I - gamma * I
dR <- gamma * I
return(list(c(dS, dI, dR)))
})
}
beta和gamma的取值同上一方法,取\(beta = 0.2586\)和\(gamma = 0.0821\)。
这里假定时间范围为\([0,150]d\),人群总数为\(N=10^6\),初始有\(999999\)位易感者,\(1\)位感染者,各个初始状态同时除以人群总数\(N\)以标准化,使得解集在\([0,1]\)范围内。
1 | init_state <- c(S = 1 - 13e-8, I = 13e-8,R = 0) |
可视化数据:
1 | ggplot(out, aes(x = time)) + |
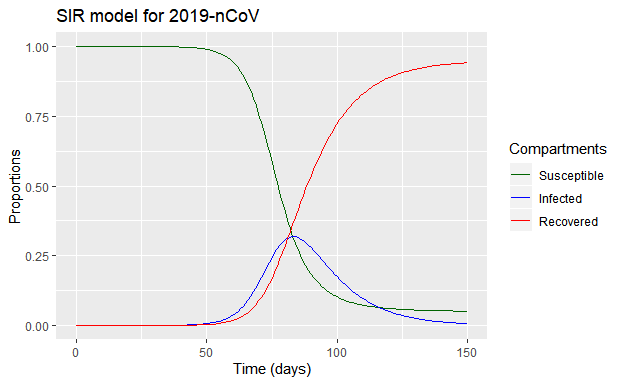
可以看到,疫情大约在发展了80天左右开始出现下行趋势。从《新型冠状病毒感染的肺炎在中国武汉的初期传播动力学》一文中得知,2019年12月中旬已出现人际传播现象;再根据2019-nCov最长潜伏期为14天,假设第一位感染者出现在2019年12月1日,则疫情开始减弱的时间为2020年2月19日。
拓展:SEIQR模型
简述
该模型在SIR模型的基础上增加了两个过程,分别是:
E(Exposed): 潜伏者,具有传染能力Q(Quarantined): 隔离者,无法传染给他人
graph LR A["S(易感)"] --"beta_1 & beta_2"--> B["E(潜伏)"] B--"epsilon"--> C["I(感染)"] C --"Delta"--> D["Q(隔离)"] D --"d"--> E["R(康复)"] D --"alpha_2"--> F["死亡"] C --"gamma"--> E C --"alpha_1"--> F
分析
基本假设
- 不考虑种群自然出生死亡率,种群个体总数为常数
N; - 增加潜伏个体数为
E(t),隔离个体数为Q(t); - \(\beta_1\)、\(\beta_2\)分别表示潜伏、感染者的传染率;
- \(\alpha_1\)、\(\alpha_2\)分别表示感染、隔离者的因病死亡率;
- \(\gamma\)、\(d\)分别表示感染、隔离者的恢复率;
- \(\epsilon\)为潜伏者发病比例,\(\frac{1}{\epsilon}\)为平均潜伏期;
- \(\delta\)为隔离比例,反映了隔离的强度;
- 在有限的人群中:\(N=S(t)+E(t)+I(t)+Q(t)+R(t)\);
- 其余条件同SIR模型基本假设。
建立方程
\[ \frac{\partial{S(t)}}{\partial{t}}=-\beta_1 S(t)E(t)-\beta_2 S(t)I(t);\;S(0)=S_0 \]
\[ \frac{\partial{E(t)}}{\partial{t}}=\beta_1 S(t)E(t)+\beta_2 S(t)I(t)-\epsilon E(t);\;E(0)=E_0 \]
\[ \frac{\partial{I(t)}}{\partial{t}}=\epsilon E(t)-(\alpha_1+\delta+\gamma)I(t);\;I(0)=I_0 \]
\[ \frac{\partial{Q(t)}}{\partial{t}}=\delta I(t)-(\alpha_2+d)Q(t);\;Q(0)=Q_0 \]
\[ \frac{\partial{R(t)}}{\partial{t}}=\gamma I(t)+dQ(t);\;R(0)=R_0 \]
\[ N=S(t)+E(t)+I(t)+Q(t)+R(t) \]
求解模型
使用deSolver求解上述初值问题:
构造SEIQR函数: 1
2
3
4
5
6
7
8
9
10
11
12
13library(deSolve)
library(ggplot2)
seiqr <- function(time, state, params){
with(as.list(c(state, params)), {
dS <- -beta_1 * S * E - beta_2 * S * I
dE <- beta_1 * S * E + beta_2 * S * I - epsilon * E
dI <- epsilon * E - (alpha_1 + delta + gamma) * I
dQ <- delta * I - (alpha_2 + d) * Q
dR <- gamma * I + d * Q
return(list(c(dS, dE, dI, dQ, dR)))
})
}
设定参数值并求解: 1. 这里同样设定人群总人数\(N=10^6\),初始只有1位感染者; 2. 由于相关数据并不清晰,因此假设潜伏期与感染期的传染能力相同,即\(\beta_1=\beta_2\) 3. 通过近期相关数据,由于感染者得不到很好的医治和隔离,因此取湖北省最高日死亡率作为感染者因病死亡率\(\alpha_1=0.053\);而假定隔离者能够得到好的医疗救治,因此取全国日死亡率作为隔离这因病死亡率\(\alpha_2=0.021\); 4. 取感染、隔离者康复率分别为\(\gamma=d=0.0821\); 5. 根据平均潜伏期为6-7天,计算出日发病比例\(\epsilon=0.155\); 6. 暂时将隔离比例定为\(\delta=0.7\)
1 | init_state <- c(S = 1 - 1e-6, E = 0, I = 1e-6, Q = 0, R = 0) |
数据可视化
1 | ggplot(out, aes(x = time)) + |
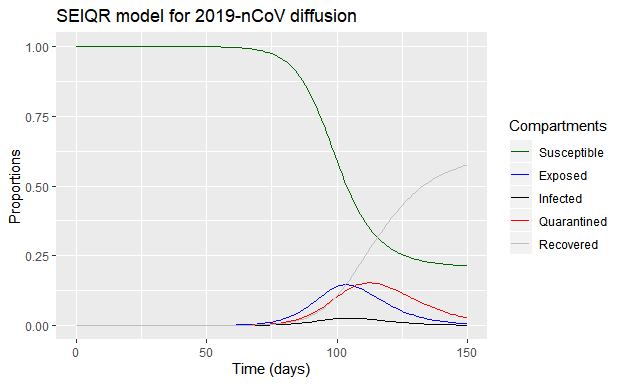
可以看出,在该模型参数下:
- 疫情减弱大约在发展100天后开始,也就是2020年3月10日。在不考虑发展中期限制交通等措施和隔离比例增加,病毒变异的情况下,感染者和潜伏着在此时达到峰值;之后在疫情发展约120天时,隔离人数达到峰值;
- 疫情结束约在疫情发展150天,也就是2020年3-4月份。
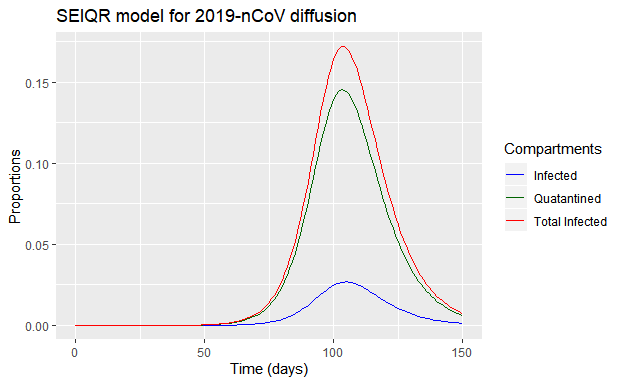
我们还可以看看在这个模型下,全体感染者(\(E(t)+I(t)\))与已知感染者(\(Q(t)\),假设会对全部被人发现的感染者采取隔离措施。)之间有何数量关系:
1 | out$TI <- out$E + out$I |
1 | # plot the diffusion of 2019-nCoV |
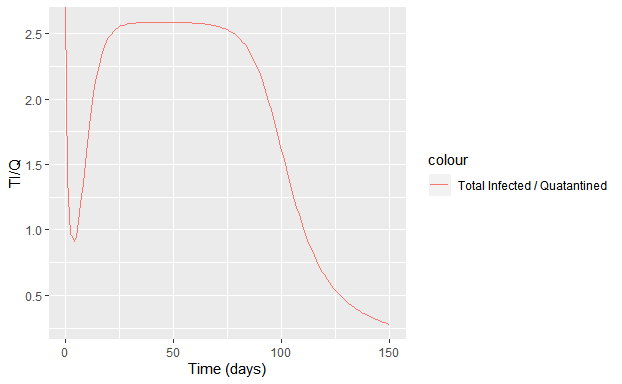
可以看到,当前时间段,实际感染者约为已发现感染者(也即隔离者)的2.6倍。
参考文献
- 《网络科学:原理与应用》Ted G. Lewis著, 机械工业出版社, 2013年7月第1版
- deSolver方法代码来源:https://github.com/wuhsiang/2019-nCoV-diffusion
- 徐翠翠, 赫孝良. 一类具有潜伏期和隔离项的SEIQR流行病模型[J]. 商丘师范学院学报, 2010(06):49-55.