C语言Ⅰ_杂记
杂记
目录
[TOC]
引用头文件
1 |
#include <> 引用的是编译器的类库路径里面的头文件。
#include "" 引用的是程序目录的相对路径中的头文件,如果在程序目录没有找到引用的头文件,则到编译器的类库路径的目录下找该头文件。
#define 、#if、#ifdef、#ifndef 作用和区别
#define
宏定义指令。
1 |
|
#if条件编译
宏编译指令。
1 |
|
作用为:如果常量表达式为真(非0),则编译程序段1,反之,编译程序段2。
#ifdef
即:if define <标识符>
1 |
|
作用为:如果标识符已经被定义过,则编译程序段1,反之,编译程序段2。
#ifndef
即:if not define <标识符>
1 |
|
作用为:如果标识符还没有被定义过,则编译程序段1,反之,编译程序段2。
#ifndef、#define、#endif避免重复引用
为防止头文件被重复引用(include嵌套,即引用的头文件里又有引用),在头文件中使用#ifndef、#define和#endif来避免。
1 |
|
小技巧:
在有多个 .h 文件和多个 .c 文件的时候,往往我们会用一个 global.h 的头文件来包括所有的 .h 文件,然后在除 global.h 文件外的头文件中 包含 global.h 就可以实现所有头文件的包含,同时不会乱。方便在各个文件里面调用其他文件的函数或者变量。
1 |
|
一些头文件
stdio.h
定义了一些输入输出函数、三个变量类型、宏。
stdlib.h
定义了一些通用工具函数、四个变量类型、宏。
itoa()数字转字符数组
atoi字符数组转数字
string.h
定义了一些字符数组处理函数、一个变量类型、一个宏。
strlen():返回字符数组中字符的数量(原理为识别空字符)。(与sizeof()的不同)
math.h
定义了各种数学函数、一个宏。
这个库中所有可用的功能都带有一个 double 类型的参数,且都返回 double 类型的结果。
pow()幂次
sqrt()开方
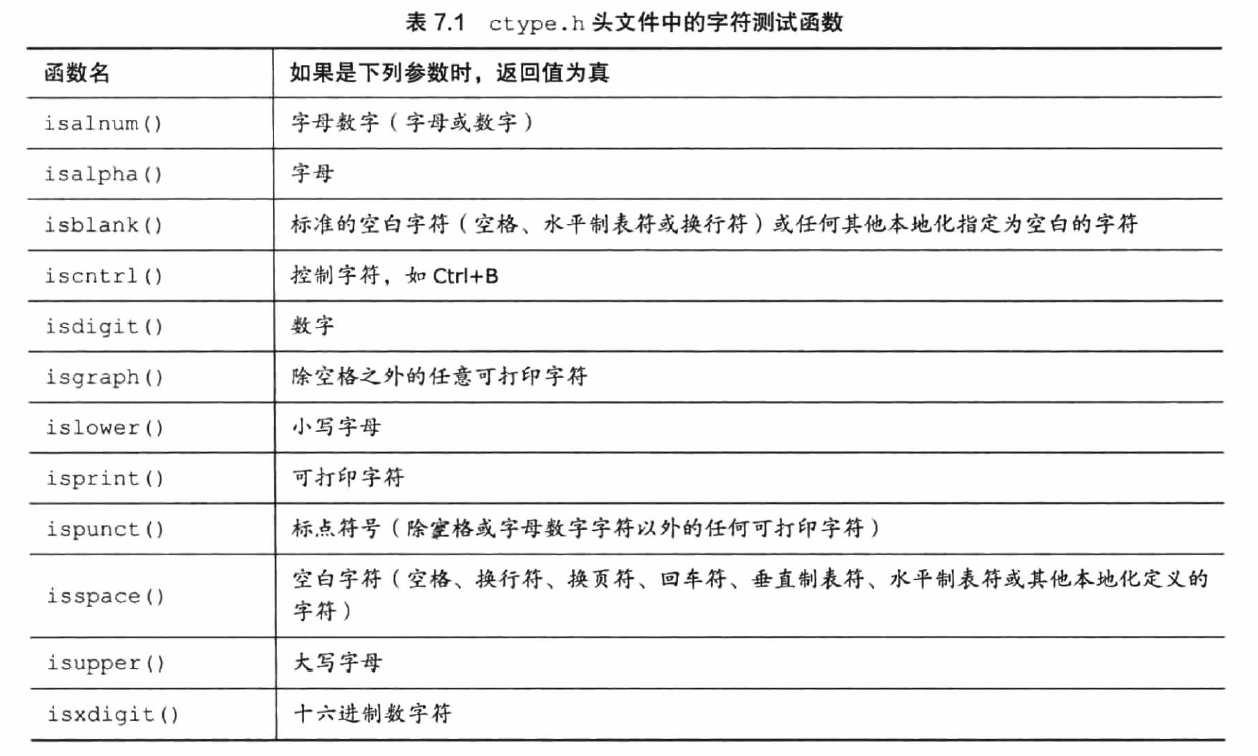
ctype.h
定义了专门处理单个字符的函数。

iso646.h
C99标准添加的备选拼写。

strlen()与sizeof()
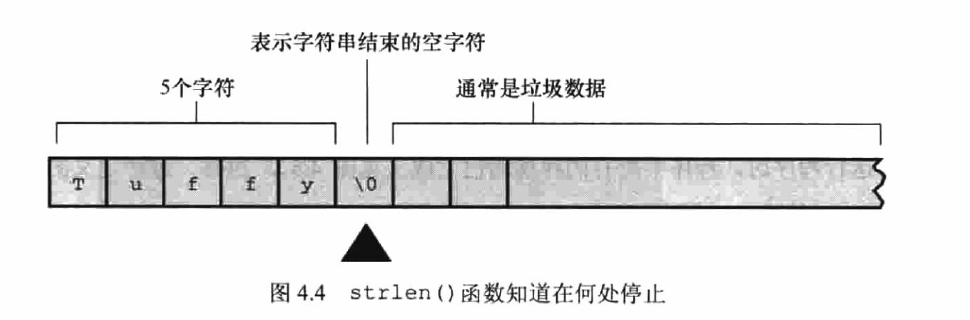
strlen()识别空字符\0来返回字符数量;
sizeof()返回对象的大小(byte),是一个size_t(无符号整型)数据类型;
可以通过
%zd输出size_t类型,或者使用%u或%lu。
1 |
|
sizeof作用与对象时需要有圆括号sizeof(int),而作用与变量时不用sizeof name,但推荐统一使用圆括号sizeof()。、
printf()对于sizeof()有%zd格式转换说明符。
图示如下:
常量与C预处理器
==如何使用常量?==
一、#define
1 |
使用预处理器,在编译时替换(compile-time substitution),称为明示常量(manifest constant)或符号常量。
所谓manifest是指在程序开头就已经显示出来的不变量。
二、const
1 | double pi; |
限定变量为只读属性。
printf()参数传递机制
示例
1 | float n1; /*传递时作为double类型*/ |
原理
1、程序将参数放入栈(stack)中(大小按照参数变量类型);
因此:n1占8 byte(转换成double类型);n2占8 byte;n3、n4占4 byte。
2、根据转换说明从栈(stack)中读取值;
因此,第一个%ld读取前4 byte,再作为long int解释;以此类推。
所以,示例代码中第一个%ld为n1的前半部分,第二个%ld为n1的后半部分,并且解释为long int。
参数传递原理.png)
printf()返回值
printf()具有返回值,返回打印字符的个数,若输出错误,则返回-1。
在写入文件的时候很常用,用来检查错误。
打印长字符串
重点在于换行方式。
- 多个
printf(); - 使用
\换行; - 多个双引号
""
scanf()输入细节
scanf默认从第一个非空白字符开始,遇到第一个空白(空格、制表符、换行符)就停止输入。
原理
我们假设使用scanf()读取几个%d格式的数据:
1 | scanf("%d %d",&a, &b); |
- 如果第一个非空白字符就是希望读取到的符号
+/-或数字,那么就保存并继续读取数字;直到读取到非数字字符,就将它放回输入流。
如果使用字段宽度,则在空白处或字段最后结束读取。
这就意味着,当scanf()读取完数字时,下一次读取的第一个就是上一次被放回输入流的非数字字符。
1 |
|
- 如果第一个非空白字符不是希望读取到的数字,而是字符
'A',则放回输入,等待下一个格式转换说明符。
当有多个格式转换说明符时,第一次出错
scanf()就会停止。
格式化输入
当格式说明符中有其他字符时,输入需要严格按照格式说明符中的字符。
1 | scanf("You are %d.",&age); |
返回值
scanf()返回值为成功输入的项数,如果出错,则返回0。
特殊用法
1 | status = scanf("%ld",&num); |
使用scanf()的返回值作为判断是否成功输入的状态码。
printf()和scanf()的*参数
printf()的*
用来通过程序指定字段宽度或浮点数精度。
1 | int width = 3, age = 5; |
通常用来格式化输出。
scanf()的*
用来跳过相应的输入项。
1 | scanf("%*d %d",&a, &b); |
这说明程序跳过了读取第一个%d对应的输入,将第二个输入拷贝给了最先的变量。
typedef
给现有数据类型创建别名。
1 | typedef float real; |
缓冲区与字符输入输出
==输入可以分为缓冲输入与无缓冲输入。==
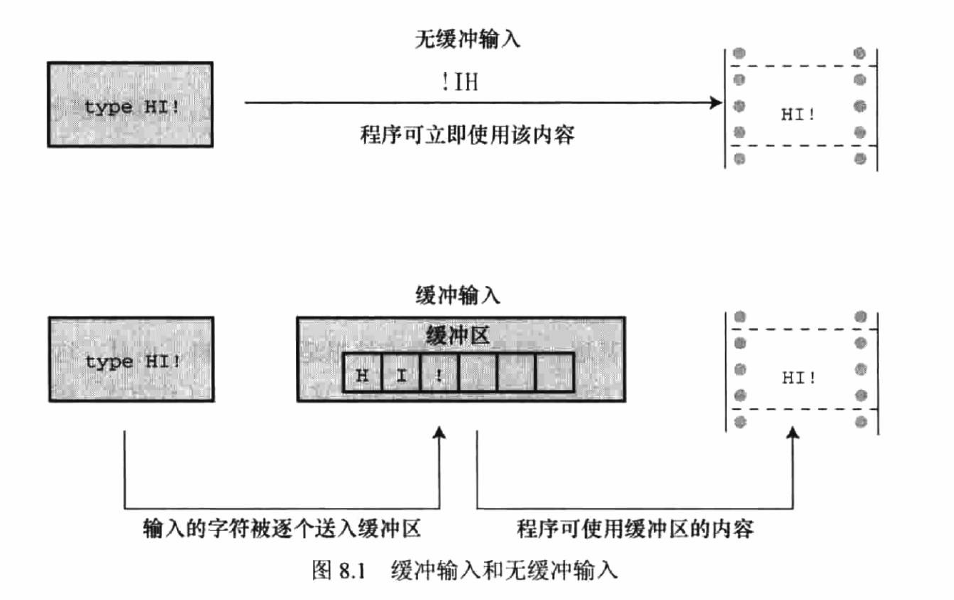
缓冲输入使用缓冲区,使得用户输入时能够更改错误的内容,并且节约传输时间(字符块发送快于单个字符发送)。
==缓冲可分为完全缓冲与行缓冲。==
完全缓冲:当缓冲区满时刷新缓冲区;
行缓冲:当读取到换行符时刷新缓冲区。
超长字符输入
由于输入的字符超级长(例如10000000个),使用scanf()或者gets()之类的函数一次读入会造成输入缓冲区溢出,这时候怎么办呢?
可以使用while((ch = getchar()) != '\n')来循环读入单个字符;
高精度PI的计算
目前我能想到的方法只有通过特殊函数的幂级数展开或者特殊数列极限来计算PI,而且很难控制精确的小数点位数。
分别使用\(\arcsin(x)=x+\sum_{n=1}^{\infty}\frac {(2n-1)!!}{(2n)!!}x^{2n+1}\)、\(\sum_{n=1}^{\infty} \frac 1{n^2}=\frac {\pi^2}{6}\)、\(\arctan(x)=\sum_{n=0}^{\infty}\frac {(-1)^n}{2n+1}x^{2n+1}\)来计算高精度\(\pi\)。第一种方法因为双阶乘计算量大,所以计算速度很慢;第二种方法由于分母含有平方项,当\(n\)很大时即使使用
long double也会造成浮点数下溢;第三种方法由于分母为一次项,能够在n很大时逼近\(\pi\)而不出现浮点数下溢。
网络上找到使用双向链表来计算指定保留小数点位数的PI值的算法,留待学习。
随机数
伪随机
梅森旋转算法
==Waiting==
线性同余法
\[ \begin{align*} &y=(ax+b)\mod m\\ &a,b,m为常数 \end{align*} \]
因此随机数的产生决定于x,即seed。
Seed需要程序中设定,一般情况下取系统时间作为种子。它产生的随机数之间的相关性很小,取值范围是0—32767(int),即双字节(16位数),若用unsigned int 双字节是65535,四字节是4294967295,一般可以满足要求。
m是模数,a是乘数,c是增量,x为初始值。
当\(c=0\)时,称此算法为乘同余法;若\(C≠0\),则称算法为混合同余法。
当
c取不为零的适当数值时,有一些优点,但优点并不突出,故常取\(c=0\)。
模m的大小是发生器周期长短的主要标志,常见有:
m为素数,取a为m的原根,则周期 T = m - 1。例如:a=1220703125、a=32719(程序中用此组数)、a=16807- \(m=2^L(L\geq4)\),\(x_0\)为奇数,取 \(a=3或5(\mod8)\),则 \(T=2^{L-2}\)
帐篷映射
分段线性映射,也是一个二维混沌映射,广泛运用在混沌加密系统中(如:图像加密),并且在混沌扩频码的产生、混沌加密系统构造和混沌优选算法的实现中也经常被使用。
\(\mu\in[0,2]\)时,成为\([0,1]\)区间上的自映射,可以定义离散时间动态系统
混沌系统是指在一个确定性系统中,存在着貌似随机的不规则运动,其行为表现为不确定性、不可重复、不可预测,这就是混沌现象。混沌是非线性动力系统的固有特性,是非线性系统普遍存在的现象。按照动力学系统的性质,混沌可以分成四种类型:时间混沌、 空间混沌、时空混沌、功能混沌。
\[ X_{n+1}=\mu \min{ \{X_n,1-X_n\} },\;X_{n} \in [0,1] \]
以下在 \(\mu=2\) 讨论: \[ X_{n+1}=1-2|X_n-\frac 12| \] 其非周期轨道点的分布密度函数为 \(\rho(x)=1,x\in (0,1)\),周期轨道点周期 \(T=2*5^c,c \in N^*\) 可以利用其周期轨道产生统计性质优良的均匀分布随机数。
定理1:不动点为\(x_1^*=0,x_2^*=\frac 23\)
==Waiting==
定理:若\(\xi \sim U(0,1)\),\(\eta=1-2|\xi-\frac 12|\),则\(\eta \sim U(0,1)\)
算法:
- 线性同余法(
LOG)产生随机数 \(X_{n+1}=AX_n+C(\mod M)\); - 取 \(W_{n+1}=2X_{n+1}(X_{n+1}\leq \frac M2)\)
- 取 \(W_{n+1}=2(M-X_{n+1})+1(X_{n+1} > \frac M2)\);
- 得到 \(Y_{n+1}=\frac {W_{n+1}}{M}\)。
平方取中法
冯诺依曼提出,取长度为2s的初始值,通过平方运算扩大差异,得到4s长的数字(不足位数补0),再取数字中间2s位数作为下次迭代初始值。
缺点:周期不确定,不稳定,容易退化为常数。
推广:乘法取中法(\(x_{n}*x_{n-1}\))、常数取中法(\(k*x_n\))
==可用于hash函数==
产生符合某种分布的随机数:
- 中心极限定理(大数定理)
- 概率分布函数的反函数
- 特殊算法
- 极限近似法
- 离散逼近法
- 舍选法
- 随机变量函数法
符合正态(高斯)分布的随机数
- 最简单实现的是利用林德伯格-莱维中心极限定理:
\({X_n}\)为独立同分布的随机变量序列,存在期望与方差。 \[ \begin{align} &Y_n^*=\frac {\sum_{m=1}^{n}X_m-n\mu}{\sigma \sqrt n} \\ &\lim_{n \to \infty}P(Y_n^*\leq y)=\Phi(y)=\frac {1}{\sqrt {2\pi}}\int_{-\infty}^{y}e^{-\frac {t^2}{2}} \,\rm {d}t \end{align} \] 取\(\mu=E(x_i),\sigma^2=Var(x_i)\),得到标准正态分布\(N(0, 1)\)。
算法过程:
- 产生\((0,1)\)上\(n\)个均匀分布的随机数,记为\(x_1,x_2,...,x_n\);(\(\mu^{'}=\frac 12,\sigma^{'}=\frac{b-a}{\sqrt{12}}\))
- 计算\(y=(\sum_{i=1}^{n}x_i-\frac n2)/((b-a)\sqrt{\frac{n}{12}})\),则\(Y\sim N(0,1)\);
- 取\(z=\mu+\sigma y\),得到\(Z\sim N(\mu,\sigma^2)\)
- 其次是一种神奇的算法—— Box-Muller算法
(比较常用的方法)
Box-Muller映射 \[ \begin{cases} Y_1=\cos{(2\pi X_2)}\sqrt{-2\ln{X_1}}\\ Y_2=\cos{(2\pi X_1)}\sqrt{-2\ln{X_2}} \end{cases} ,\;X_1,X_2\sim U(0,1) \] 则\(Y_1,Y_2\)服从标准正态分布\(N(0,1)\)。
则\(Z=\mu+\sigma Y\sim N(\mu,\sigma^2)\)
符合指数分布的随机数
概率分布函数的反函数。
负数除法
在计算机中,计算采用原数的补码来完成。
原码、反码与补码
对于int类型,计算-2147483648 / -1的结果,程序运行出错,
文件结尾EOF与数据类型
char –> EOF
unsigned char –> 255
int –> -1
读写文件的函数
在函数内修改指针
那么我们传入的应该是指针的指针,将修改的指针值作为被解引用的变量值。
